Basics of NLP

Posted on | In
Stand on the shoulders of giants.

Basics of NLP

Introduction

Basically, the supervised learning tasks of NLP can be divided into three major parts:

  • Data collection and preprocessing
  • Feature extraction and encoding (CNN, RNN, Transformer)
  • Model design for specific task

Sometimes the second and the third task are closely related to each other. For example, most sequence-to-sequence models have a encoder and a decoder. Decoder is more like a task-specific model, and encoder can be adjusted based on decoder, like adding attention. However, sometimes the encoder and decoder part may not be connected so tightly. For example, for some text classification problem, encoder takes responsibility for extracting the feature of text data. If we add some fully-connected layers and softmax layer on the top of encoder, we can regard this whole model as a task-specific model for text classification.

Since most NLP tasks can be solved using the above three parts, and data preprocessing and task-specific model need to be designed based on different tasks, can we have a pool of encoder models that can be utilized as generalized module? Let’s think about some computer vision tasks. Many of models for these tasks using pre-trained model from ImageNet. It is convenient to use pre-trained model as an encoder to save computational cost and improve decoder performance. Similarly, can we discover a generalized encoder model in NLP field?

The shoulders of giants in CV

In 2012, AlexNet was invented and achieved high accuracy for image classification problem.

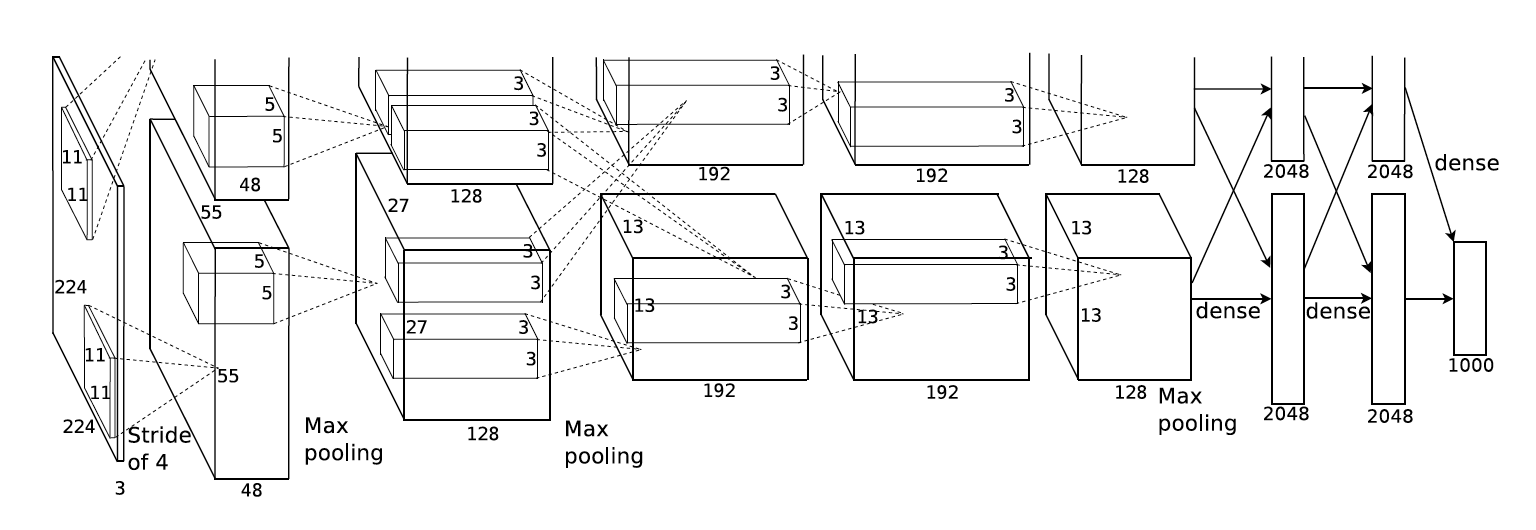fig. 1 After that, people found that using pre-trained model in their own models can significantly improve their performance in many new tasks, such as object detection and image segmentation.

Why this training pattern works? The Google Brain group analyzed and visualized the intermediate layers of GoogleNet, and found that the lower layers can learn the texture and edge of object, while the high-level layer can learn the object itself. Generally speaking, edge is a common feature among objects. Therefore, if we use pre-trained network to initialize our own models, then we won’t need to learn those parameters from scratch, or maybe we just need do fine-tuning on the pre-trained network, which improves the training efficiency.

fig. 2

Where is the shoulders of giants in NLP

Intuitively, we want to extract the meaning behind language data, and convert it to a feature that computers can understand.

Traditional ways to convert textual features to inputs

Before word2vec, people tried many ways to represent text data. They use one-hot encoding to represent a word and bag-of-words to represent a sentence. They use TFIDF to identify the importance of word among documents. They used text-rank to give each word a weight. (Here I want to add SVD->LSA, pLSA and LDA in the future.)

language model

In fact, language model is a probability distribution over sequences of words. If $S_i$ is a sequence of words, we want to calculate $P(S_i) = \frac{c(S_i)}{\sum_{j=0}^{\infty}{c(S_j)}}$.

This equation is simple, however, it is impossible to compute the probability on all the sequences of words along the history in the world. Therefore, splitting a sequence of words into individual words and computing the probability of the sequence through the probability of the appearance of word given previous words becomes a solution.

Suppose the length of sentence is T, and word is $x_i$, $P(s_i)=P(x_0, x_1, …, x_T) = P(x_0)P(x_1 x_0)P(x_2 X_0,x_1)…P(x_T x_0,x_1,x_2,…,x_{T-1})$.
However, this equation is still difficult to compute. Therefore, we would introduce Markov Assumption, which assumes that the conditional probability distribution of future states of the process depends only on the present state, not on the sequence of events that preceded it. So we suppose that the future word only depends on the previous n words. Therefore, when $n =1$, the above equation can be represented as $P(S_i)=P(x_0, x_1, …, x_T)=P(x_0)P(x_1 x_0)P(x2 x1)…P(x_T x_{T-1})=P(x_0)\prod_{i=0}^{T-1}P(x_{i+1} x_i)$. Also, we can use $P(x_{i+1} x_i)=\frac{c(x_{i+1},x_i)}{c(x_i)}$ to compute the conditional probability.

However, this model has some problems.

  1. $c(x_{i+1},x_i)$ can be zero especially when n is big. Hence we need to use some smoothing techniques.
  2. if n is a great number, then the computation cost would increase, we usually use 3-gram. However, this means that the language model cannot model relationship of long context.
  3. This model cannot find the similarity among words.

NNLM (Neural Net Language Model)

fig. 3

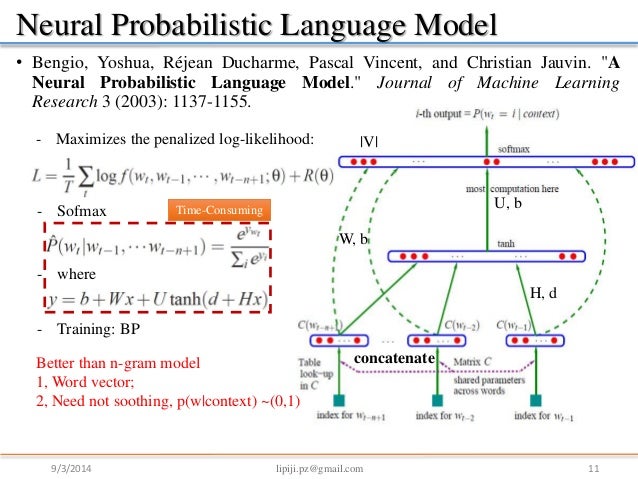
We can divide this model into three parts.

  1. from word to vector x through matrix C
  2. from vector x to hidden layer through matrix H
  3. from hidden layer to output layer through matrix U
  4. from x to output layer through matrix W.

$y = b + Wx + Utanh(d + Hx)$

$x = (C(w_{t-1}), C(w_{t-2}), …, C(w_{t-n+1}))$ x is a m-dimensional vector which computed from each input word w, then concatenate n-1 words, we can get a (n-1)*m matrix.

This work inspired the thought of word2vec.

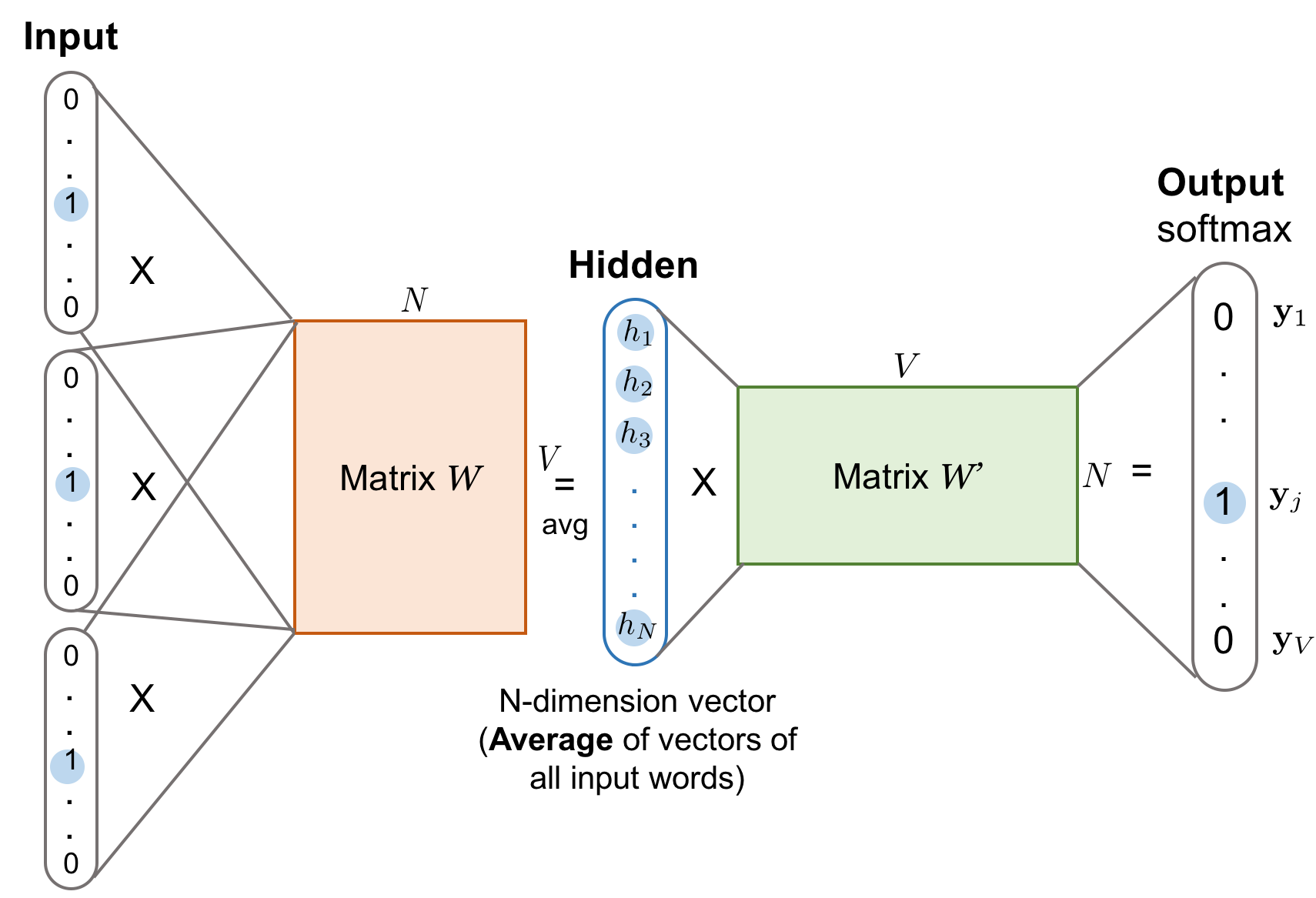
CBOW and skip-gram

CBOW is continuous Bag-of-Words. CBOW model doesn’t have hidden layer. fig. 4